Олимпиада (фев 2016, математика) 7-8 классы - задачи и ответы

1. Число 10¹⁰⁰ назовем великан. Чему равно число 1000¹⁰⁰?

Решение:
1000¹⁰⁰ = (10³)¹⁰⁰ = (10¹⁰⁰)³ = великан³.

Ответ: великан³

2. Сколько простых чисел, меньших 2016, имеют сумму цифр, равную двум?

Решение:
Таких чисел только три: 2, 11 и 101.

Ответ: 3

3. На плоскости отметили 10 точек, затем каждые две из них соединили отрезком. Какое наибольшее число таких отрезков может пересечь прямая, которая не проходит ни через одну из этих точек?

Решение:
Наибольшее число отрезков, которые пересекает прямая, будет, если с одной стороны от прямой находятся 5 точек и с другой стороны - тоже 5 точек.

Ответ: 25

4. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 20 минут папа заметил пропажу, быстро развернул лодку, и они поплыли вниз по течению с той же собственной скоростью. За сколько минут они догонят шляпу?

Решение:
Можно считать, что в реке никакого течения нет. Тогда шляпа стоит на месте, а лодка отплывает от шляпы в течение 20 минут, а потом возвращается назад с той же скоростью.

Ответ: 20

5. Света выбрала двузначное число, не делящееся на 10, поменяла его цифры местами и вычислила разность полученных чисел. Какое самое большое число она могла получить?

Решение:
10a + b – 10b – a = 9(a – b).
Поскольку a и b не равны 0, данное выражение принимает наибольшее значение при a = 9 и b = 1, оно равно 72.

Ответ: 72

6. Назовем старшим делителем числа самый большой из его делителей, не равный самому числу, а младшим делителем назовем самый маленький делитель, не равный 1. Например, у числа 12 старший делитель равен 6, а младший равен 2. Сколько существует чисел, у которых старший делитель в 15 раз больше младшего?

Решение:
Произведение старшего делителя на младший делитель некоторого числа равно самому числу. Если старший делитель числа в 15 раз больше младшего, то младший делитель может быть равен 2 или 3. Действительно, число делится на 15, а значит, и на 3.
Таким образом, возможно только два варианта: число равно 2·2·15 = 60 или 3·3·15 = 135.

Ответ: 2

7. Каждая из трех окружностей на чертеже касается двух других. Радиус большей окружности равен 6. Какова сумма расстояний между центрами?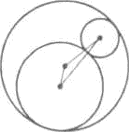

Решение:
Обозначим A центр большой окружности, B центр средней окружности, C центр меньшей окружности.
Пусть радиус меньшей окружности равен х, радиус средней окружности равен y.
Тогда АВ + ВС + АС = (6 – у) + (х + у) + (6 – х) = 12.

Ответ: 12

8. За 5 лет обучения студент сдал 31 экзамен, причём в каждом году он сдавал экзаменов больше, чем в предыдущем. На пятом курсе экзаменов втрое больше, чем на первом. Сколько экзаменов на четвёртом курсе?

Решение:
Возможен только следующий вариант: на первом курсе 3 экзамена, на втором - 5, на третьем - 6, на четвертом - 8, на пятом - 9.

Ответ: 8