Олимпиада (ноя 2020, математика) 9-10 классы - задачи и ответы
1. Найдите первую цифру наименьшего из чисел, которые делятся на 4 и имеют сумму цифр 1000.
РЕШЕНИЕ
Наименьшим из чисел, которые делятся на 4 и имеют сумму цифр 1000, является число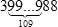
Ответ: 3
2. На окружности отметили 7 красных и 8 зеленых точек и соединили каждую точку с каждой. Что получится, если из числа всех отрезков с концами разного цвета вычесть число отрезков с концами одинакового цвета?
РЕШЕНИЕ
Отрезков с концами разного цвета 56 (56 = 7·8). Отрезков с красными концами 21 (21 = 7·6/2). Отрезков с зелеными концами 28 (28 = 8·7/2). Если из числа отрезков с концами разного цвета вычесть число отрезков с концами одинакового цвета, получится 7 (7 = 56 – 21 – 28).
Ответ: 7
3. За круглым столом сидят 32 попугая: зеленые и синие. Синие попугаи всегда говорят правду, а зеленые всегда лгут. Пятнадцать попугаев сказали: «Мой сосед справа такого же цвета, как и я», а остальные сказали: «Мой сосед справа не такого цвета, как я». Сколько зеленых попугаев за столом?
РЕШЕНИЕ
Рассмотрим следующую таблицу.
| Попугай, который говорит | Его сосед справа |
| Синий – первое утверждение | Синий |
| Синий – второе утверждение | Зеленый |
| Зеленый – первое утверждение | Синий |
| Зеленый – второе утверждение | Зеленый |
Как видно из таблицы, если попугай говорит первое утверждение, то его сосед справа синий, если второе, то его сосед справа зеленый. Первое утверждение сказали 15 попугаев. Значит, 15 попугаев синие, остальные – зеленые.
Ответ: 17
4. Все натуральные числа от 1 до 100 были выписаны в таком порядке: сначала в порядке возрастания, выписали числа, сумма цифр у которых равна 1, затем в таком же порядке выписали числа, у которых сумма цифр равна 2 и т.д. На каком месте будет стоять число 68?
РЕШЕНИЕ
Сумма цифр числа 68 равна 14. В последовательности после чисел с суммой цифр 14 идут числа с суммой цифр 15, 16, 17 и 18. Рассмотрим следующую таблицу.
| Сумма цифр 2-значного числа | 14 | 15 | 16 | 17 | 18 |
| Количество таких чисел | 5 | 4 | 3 | 2 | 1 |
Числа с суммой цифр 14 идут в следующем порядке: 59, 68, 77, 86, 95. Значит, после числа 68 в последовательности находятся еще 13 чисел (13 = 1 + 2 + 3 + 4 + 3).
Ответ: 87
5. Вычислите значение данного выражения.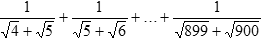
РЕШЕНИЕ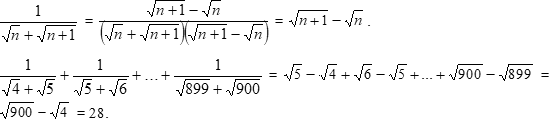
Ответ: 28
6. Электронные часы показывают часы и минуты, от 00:00 до 23:59. Сколько времени в течение суток на табло этих часов присутствует хотя бы одна цифра 1?
РЕШЕНИЕ
В сутках 24 часа. Эти часы можно разделить на два типа. Первый тип: часы, во время которых 1 имеется среди первых двух чисел на табло. В течение такого часа 1 находится на табло 60 минут. Второй тип: часы, во время которых 1 нет среди первых двух чисел на табло. В течение такого часа 1 находится на табло 15 минут. Часов первого типа 12, второго – 12. Значит, 1 будет находиться на табло 12·60 + 12·15 минут.
Ответ: 15 ч.
7. Два равных треугольника ABC и DEC расположены так, как показано на рисунке. Известно, что DC = АС = 1, СВ = СЕ = 4. Площадь треугольника АВС равна 1. Найдите площадь заштрихованной фигуры.
РЕШЕНИЕ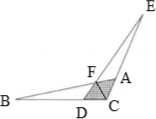 Проведем отрезок FC. Рассмотрим треугольники FDB и FDC. Эти треугольники имеют общую высоту, выходящую из вершины F. Но в первом треугольнике сторона, лежащая против вершины F в три раза больше, чем во втором. Поэтому площадь первого треугольника в три раза больше, чем площадь второго. Пусть площадь FDC равна х, тогда площадь FDB равна 3х. Треугольник АВС состоит из треугольников FDB, FDC и FAC. Значит, 3х + х + х = 1. Отсюда х = 0,2.
Проведем отрезок FC. Рассмотрим треугольники FDB и FDC. Эти треугольники имеют общую высоту, выходящую из вершины F. Но в первом треугольнике сторона, лежащая против вершины F в три раза больше, чем во втором. Поэтому площадь первого треугольника в три раза больше, чем площадь второго. Пусть площадь FDC равна х, тогда площадь FDB равна 3х. Треугольник АВС состоит из треугольников FDB, FDC и FAC. Значит, 3х + х + х = 1. Отсюда х = 0,2.
Ответ: 0,4
8. Сто парламентариев, получающих разные зарплаты, сидят в прямоугольном зале в 10 рядах по 10 кресел. Парламентарий считает себя высокооплачиваемым, если, спросив соседей справа, слева, спереди, сзади и по диагоналям, он убеждается, что зарплату, большую его зарплаты, получает не более чем один из его соседей. Какое наибольшее число высокооплачиваемых может быть среди этих парламентариев?
РЕШЕНИЕ
Присвоим парламентариям номера от 1 до 100: номер 1 – самый низкооплачиваемый парламентарий, 2 – следующий за ним и т.д. Рассадим парламентариев, как показано на рисунке. Тогда каждый из 50 парламентариев в выделенных цветом рядах будет считать себя высокооплачиваемым.
1-10 | 51-60 | 11-20 | 61-70 | 21-30 | 71-80 | 31-40 | 81-90 | 41-50 | 91-100
Докажем, что больше 50 высокооплачиваемых парламентариев быть не может. Непосредственным перебором легко установить, что в квадрате 2×2 больше двух высокооплачиваемых парламентариев быть не может. Квадрат 10×10 можно разрезать на 25 квадратов 2×2. В каждом из квадратов 2×2 не больше двух высокооплачиваемых парламентариев. Значит, всего высокооплачиваемых парламентариев не больше 50 (50 = 25·2).
Ответ: 50

