Олимпиада (ноя 2020, математика) 5-6 классы - задачи и ответы
1. В числах 345 и 921 выбрали по одной цифре и поменяли их местами друг с другом. При этом сумма чисел увеличилась. Чему стала равна эта сумма?
РЕШЕНИЕ
Cумма увеличится, только если поменять местами цифры 5 и 2.
Ответ: 1293
2. Масса стального кубика равна 30 г. Какова масса стального кубика с ребром втрое большим?
РЕШЕНИЕ
Кубик с ребром 3х можно разрезать на 27 кубиков с ребром х. Поэтому масса большого кубика равна 810 г (810 = 30·27).
Ответ: 810 г
3. На заседании присутствуют 29 академиков, 13 из них с бородой, а 18 - с усами. У троих академиков нет ни бороды, ни усов. У скольких академиков имеются и борода, и усы?
РЕШЕНИЕ
26 академиков имеют либо усы, либо бороду (26 = 29 – 3). Из них пятеро имеют и усы, и бороду (5 = 13 + 18 – 26).
Ответ: 5
4. Дворник работает по вторникам, пятницам и нечетным числам. Какое наибольшее количество дней подряд он может работать?
РЕШЕНИЕ
Дворник может работать шесть дней подряд: Понедельник (29), Вторник (30), Среда (31), Четверг (1), Пятница (2), Суббота (3).
Три нечетных числа подряд быть не может, две пары нечетных чисел с перерывом в один день быть тоже не может. Поэтому 7 дней подряд он работать не может.
Ответ: 6
5. 20 роботов собирают за 5 часов 10 стиральных машин. Сколько машин соберут 10 таких же роботов за 7 часов?
РЕШЕНИЕ
20 роботов собирают за 5 часов 10 стиральных машин. Из этого следует, что 20 роботов собирают за 1 час 2 стиральные машины. Значит, 10 роботов собирают за 1 час 1 стиральную машину. Следовательно, 10 роботов собирают за 7 часов 7 стиральных машин.
Ответ: 7
6. Электронные часы показывают часы и минуты (от 00:00 до 23:59). Сколько раз за сутки в наборе цифр на табло этих часов участвуют только цифры 2 и 3 (или одна из этих цифр)?
РЕШЕНИЕ
На первом месте может быть только цифра 2, на втором, третьем и четвертом – 2 или 3. Поэтому вариантов всего 8 (8 = 23).
Ответ: 8
7. Наименьшее трехзначное число, в котором цифр, не меньших 5, не меньше, чем цифр, меньших 5, равно...
РЕШЕНИЕ
Наименьшее трехзначное число, в котором цифр, не меньших 5, не меньше, чем цифр, меньших 5. Это можно переформулировать: наименьшее трехзначное число, в котором цифр, больших или равных 5, больше или равно, чем цифр, меньших 5. Это число 155.
Ответ: 155
8. На круговой дорожке из одной точки в противоположных направлениях стартовали одновременно Дима на велосипеде и Коля пешком. Скорость Димы в 3 раза больше скорости Коли. Дима проехал несколько кругов и за это время встретил Колю 8 раз. Сколько кругов проехал Дима?
РЕШЕНИЕ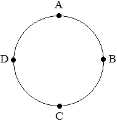 Пусть Дима и Коля отправились из точки А, Коля по часовой стрелке, Дима – против (см. рисунок). За одно и то же время Дима преодолевает расстояние, в три раза большее, чем Коля. Поэтому в первый раз они встретятся в точке В, потом будут точки C, D, A и т.д. В восьмой раз они встретятся в точке А. Коля при этом преодолеет 2 круга, а Дима – в три раза больше.
Пусть Дима и Коля отправились из точки А, Коля по часовой стрелке, Дима – против (см. рисунок). За одно и то же время Дима преодолевает расстояние, в три раза большее, чем Коля. Поэтому в первый раз они встретятся в точке В, потом будут точки C, D, A и т.д. В восьмой раз они встретятся в точке А. Коля при этом преодолеет 2 круга, а Дима – в три раза больше.
Ответ: 6

