Решение и ответы. Математика 3-4 классы
Решение и ответы
Математика 3-4 классы
Задание 1
НФайер работал в мастерской с 2 по 12 число месяца без выходных. За каждый день работы он получает 500 рублей. Сколько денег заработал Файер?
- А) 4500 рублей
- Б) 5000 рублей
- В) 5500 рублей - правильный ответ
- Г) 6000 рублей
- Д) 6500 рублей
Решение
Файер работал 11 дней. Он должен получить 5500 рублей (5500 = 11ˑ500).
Задание 2
У Дедуса на полке книги стоят в один ряд. Самая большая и самая маленькая книги стоят рядом с самой старой. Слева от самой большой — 15 книг, а справа от самой маленькой — 18 книг. Сколько всего книг может быть на полке (укажи наименьшее возможное число)?
- А) 38
- Б) 36
- В) 34
- Г) 32 - правильный ответ
- Д) 30
Решение
Пусть Б – самая большая книга, М – самая маленькая книга, С – самая старая книга. Возможны только две ситуации: 15 Б С М 18 и 16 М С Б 13. В первой ситуации количество книг 36, во второй – 32. Поэтому наименьшее число книг – 32.
Задание 3
Симка решает пример на сложение двух чисел. В примере первое слагаемое меньше суммы на 350, а сумма больше второго слагаемого на 150. Чему равна сумма?
- А) 400
- Б) 450
- В) 500 - правильный ответ
- Г) 550
- Д) 600
Решение
Первое слагаемое меньше суммы на 350. Значит, второе слагаемое равно 350. Сумма больше второго слагаемого на 150. Значит, первое слагаемое равно 150. Данный пример на сложение: 150 + 350 = 500.
Задание 4
На празднике пятеро фиксиков встали в хоровод: Симка, Нолик, Игрек, Катя и Шпуля. Мальчики стояли рядом друг с другом, а у Симки и слева, и справа стояли фиксики одного пола. Игрек встал рядом с Шпулей, потому что он в неё влюблён. Кто соседи Кати?
- А) Шпуля и Нолик
- Б) Симка и Нолик - правильный ответ
- В) Симка и Игрек
- Г) Шпуля и Игрек
- Д) Симка и Шпуля
Решение
Мальчики стояли рядом друг с другом, а у Симки и слева, и справа стояли дети одного пола. Значит, соседи Симки – это Катя и Шпуля. Игрек стоял рядом со Шпулей. Значит, они могли стоять только так:
---Н--И---
-К------Ш--
-----С-----
По схеме видно, что соседи Кати – это Симка и Нолик.
Задание 5
Дедус загадал числа. Сколько существует трёхзначных чисел, произведение цифр которых равно 48?
- А) 15
- Б) 17
- В) 19
- Г) 21 - правильный ответ
- Д) Другой ответ
Решение
Существует четыре набора цифр, удовлетворяющих условию задачи. Первый: 3, 4, 4. Второй: 2, 4, 6. Третий: 1, 6, 8. Четвертый: 2, 3, 8. Из первого набора можно составить 3 числа. Из остальных – по 6. Поэтому всего существует 21 число (21 = 3 + 6 + 6 + 6).
Задание 6
Нолик играл с числом: сначала поменял местами цифру сотен и десятков, потом десятков и единиц, а потом единиц и тысяч. В итоге получилось число 7925. Определите вторую цифру исходного числа.
- А) 7 - правильный ответ
- Б) 9
- В) 2
- Г) 5
- Д) невозможно определить
Решение
будем решать задачу с конца. Определим число до третьей операции, потов – до второй, потом – до первой. Оформим это в виде таблицы (заполняем таблицу снизу).
| Исходное число | 5792 |
| Десятки, сотни | 5972 |
| Десятки, единицы | 5927 |
| Единицы, тысячи | 7925 |
Задание 7
Шпуля вырезала часть квадрата, показанного слева. Что у неё не могло получиться?
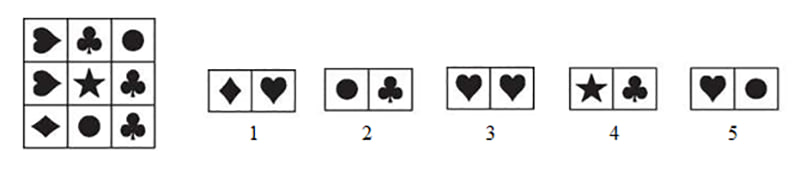
- А) 1
- Б) 2
- В) 3
- Г) 4
- Д) 5 - правильный ответ
Решение
Варианты 1-4 возможны. Вариант 5 получиться не может.
Задание 8
Верта собирает наклейки и для пополнения коллекции время от времени обменивает 1 свою редкую наклейку на 4 наклейки попроще. Изначально у неё было 7 наклеек. Сколько наклеек станет после 17 обменов?
- А) 52
- Б) 58 - правильный ответ
- В) 64
- Г) 75
- Д) другой ответ
Решение
После каждого обмена количество календариков у Верты увеличивается на 3. Поэтому после 17 обменов оно будет равно 7 + 3 + 3 + … + 3 (в сумме 17 троек).
